$$$\DeclareMathOperator{\sam}{softargmax} \def \bm#1{\boldsymbol#1} \def \R {\mathbb{R}} \def \E {\mathbb{E}} \def \V {\mathbb{V}}$

Конформация цепи во внешнем поле

Список литературы:

1. М. Дой, С. Эдвардс, "Динамическая теория полимеров", глава 2.3.
2. S. T. Milner, et. al., "A Parabolic Density Profile for Grafted Polymers", Europhys. Lett. 5, pp. 413-418 (1988).

Функция Грина

Если полимер находится во внешнем поле $\varphi (\mathit{r})$$\phi(\bm r)$, которое действует на каждый участок цепи, то равновесное распределение гауссовой цепи изменяется за счет добавления больцмановского фактора:

Соответственно, выражение для функции Грина через функциональный интеграл принимает вид:

где нормировочная константа учтена в мере интегрирования.

Напомним некоторые базовые свойства функции Грина. Из определения следует, что

где выражение под интегралом представляет собой статистический вес цепи, которая начинается в точке ${\mathit{R}}^{\prime }$$\bm R'$, проходит через точку ${\mathit{R}}^{″}$$\bm R''$ через $n$$n$ шагов и заканчивается в точке $\mathit{R}$$\bm R$.

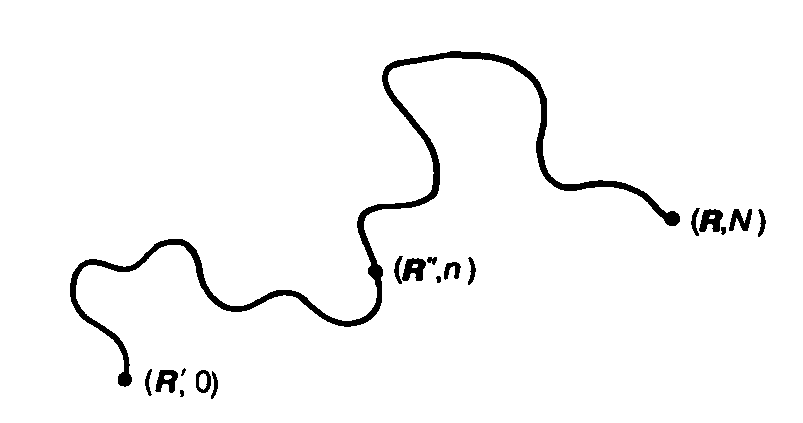
Если известно выражение для функции Грина, то можно вычислять средние значения от различных физических характеристик. Например, если величина $A$$A$ зависит только от положения $n$$n$-го сегмента, то

где выражение в знаменателе представляет собой статистический вес всех возможных конформаций цепи. Аналогичное выражение несложно записать, если физическая величина $A$$A$ зависит от положений сразу нескольких сегментов.

Математический аппарат с точностью до переобозначений эквивалентен интегралам по траекториям в квантовой механике. Поэтому функция Грина удовлетворяет дифференциальному уравнению

где произведение дельта-функций в правой части означает наложение граничных условий

Напомним, что если внешнее поле отсутсвует, то функция Грина сводится к распределению Гаусса:

Цепь в ящике

В качестве примера приминения функции Грина рассмотрим полимер, который находится в коробке объемом $V=L_x{L}_y{L}_z$$V=L_x L_y L_z$. Это означает, что внешний потенциал равен бесконечности за пределами коробки и обращается в ноль внутри.

Таким образом, нам нужно найти решение уравнения

с дополнительным граничным условием

Упражнение 1. Покажите, что функция Грина равна

$$\begin{array}{}\text{(10)}& G(\mathit{R},{\mathit{R}}^{\prime };N)=g_x(R_x,R_x^{\prime };N)g_y(R_y,R_y^{\prime };N)g_z(R_z,R_z^{\prime };N),\end{array}$$

где

$$\begin{array}{}\text{(11)}& g_x(R_x,R_x^{\prime };N)={\displaystyle \frac{2}{L_x}}\sum _{p=1}^{\mathrm{\infty }}\sin \left({\displaystyle \frac{p\pi R_x}{L_x}}\right)\sin \left({\displaystyle \frac{p\pi R_x^{\prime }}{L_x}}\right)\exp (-{\displaystyle \frac{p^2{\pi }^{2}N{b}^2}{6L_x^2}}).\end{array}$$

Указание: вспомните о решении уравнения диффузии на отрезке с поглощающими граничными условиями методом Фурье.

Теперь по известной функции Грина можно вычислить статистическую сумму для нашего полимера

где

Наконец мы можем легко вычислить свободную энергию $F=-k_{B}T\ln Z$$F=-k_B T \ln Z$ и с ее помощью определить давление, которое действует на стенку, перпендикулярную $x$$x$-направлению:

Короткий полимер, $\sqrt{N}b\ll L_x,L_y,L_z$$\sqrt{N} b \ll L_x, L_y, L_z$

В этом предельном случае находим

и получаем $P_x={\displaystyle \frac{k_{B}T}{L_x{L}_y{L}_z}}$$P_x = \dfrac{k_B T}{L_x L_y L_z}$, то есть $P_{x}V=k_{B}T$$P_x V = k_B T$. Аналогичным образом нетрудно показать, что $P_x=P_y=P_z$$P_x=P_y=P_z$, то есть давление изотропно и мы получаем аналог уравнения состояния для идеального газа.

Упражнение 2. Покажите, что

$$\begin{array}{}\text{(16)}& \sum _{p=1,3,\dots }^{\mathrm{\infty }}{\displaystyle \frac{1}{p^2}}={\displaystyle \frac{{\pi }^2}{8}}.\end{array}$$

Длинный полимер, $\sqrt{N}b\gg L_x,L_y,L_z$$\sqrt{N} b \gg L_x, L_y, L_z$

В случае длинного полимера доминирующий вклад в статистическую сумму вносит первое слагаемое, поэтому находим

что приводит к следующему выражению для давления:

Таким образом, давления в разных направлениях не равны друг другу (если $L_x\ne L_y\ne L_z$$L_x \neq L_y \neq L_z$).

Оптимальная конформация полимерной щетки

Если внешний потенциал достаточно сильный, а температура низкая, то наиболее вероятная конформация полимерной цепи соответствует минимуму величины (вспомните лекцию про оптимальную флуктуацию)

Структура этого выражения эквивалентна действию в классической механике: контурная длина вдоль полимера $\tau$$\tau$ играет роль времени $t$$t$, $3/b^2\to m$$3/b^2 \to m$, $\dot{\mathit{r}}\to \mathit{v}$$\dot{\bm r} \to \bm v$, $\varphi (\mathit{r})/k_{B}T\to -U(\mathit{r})$$\phi(\bm r)/k_B T \to - U(\bm r)$. Поэтому седловая/оптимальная конформация удовлетворяет уравнению Эйлера-Лагранжа/Ньютона:

Рассмотрим щетку, которая представляет из себя большое количество полимеров, прикрепленных одним концом к плоской поверхности. Будем следить за отдельным полимером.

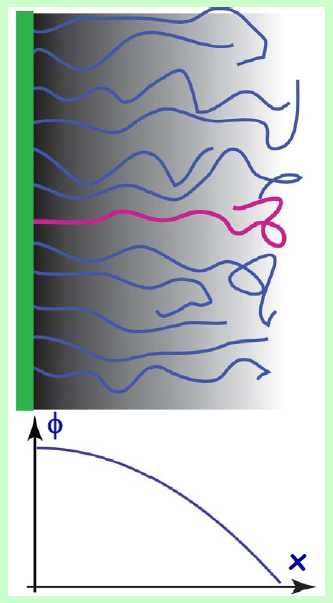
Он не может изгибаться вблизи точки прикрепления из-за давления со стороны остальных полимеров, поэтому он стремится к лучшей жизни и его второй конец пытается отдалиться от поверхности. Можно сказать, что полимер находится в некотором среднем самосогласованном поле $\varphi (x)$$\phi(x)$, которое создают его соседи. Здесь $x$$x$ – координата в направлении ортогональном плоскости. В других направлениях задача обладает трансляционной инвариантностью и эти степени свободы могут быть исключены из рассмотрения. Как же устроено это поле $\varphi (x)$$\phi(x)$?

Изохронный маятник

Все полимеры в нашей щетке находятся в одинаковых условиях. Про любой полимер можно думать как про частицу, которая в момент времени $t=0$$t=0$ находится на поверхности $x=0$$x=0$ и которая удаляется на расстояние $x=h$$x=h$ (различному для разных полимеров) к моменту времени $t=N$$t=N$.

Получается что время (период колебаний) не зависит от удаления $h$$h$ (амплитуды) – это верно ТОЛЬКО для гармонического осциллятора, поэтому $\varphi (x)\propto -x^2$$\phi(x) \propto -x^2$. Мы даже можем найти коэффициент пропорциональности, поскольку четверть периода колебаний равняется длине полимера $N$$N$:

В итоге приходим к выражению для потенциала

Закон сохранения энергии

Уравнение движения для нашей частицы/полимера можно записать в виде закона сохранения энергии (см. выше), поэтому приходим к соотношению:

Здесь энергия $E$$E$ определяется из условия, что частица достигает расстояния $x=h$$x=h$ с нулевой скоростью. Другими словами, это означает, что натяжение полимера равно нулю на конце. В результате для скорости получаем выражение

Плотность полимеров

Число мономеров $\delta \tau$$\delta \tau$ на интервал высоты $\delta x$$\delta x$ равно (линейная плотность) $\delta \tau /\delta x$$\delta \tau/\delta x$, то есть эта величина равна обратной скорости:

Интеграл от нее как и следует ожидать равен полному числу мономеров $N$$N$.

Упражнение 3. Покажите, что для полимера со свободным концом при $x=h$$x=h$ мономер с номером $s$$s$ расположен в среднем на высоте $x^{\ast }=h\sin (\pi s/2N)$$x^* = h \sin (\pi s/2N)$.

Решение. Это следует из соотношения

$$\begin{array}{}\text{(26)}& {\displaystyle \frac{2N}{\pi }}{\int }_0^{x^{\ast }}{\displaystyle \frac{dx}{\sqrt{h^2-x^2}}}=s.\end{array}$$

Разные полимеры заканчиваются на разных удалениях $x=h$$x=h$ от поверхности. Если $\sigma$$\sigma$ – число полимеров на единицу площади, то

где $H$$H$ – максимально возможное значение $h$$h$, а $\psi (h)$$\psi(h)$ – доля полимеров, которые заканчиваются при $x=h$$x=h$. Обе эти величины следует определять из условия самосогласования.

Самосогласование

Условие согласования связывает потенциал $\varphi (x)$$\phi(x)$ с плотностью полимеров $\rho (x)$$\rho(x)$. Мы будем полагать, что в нашем случае эта связь имеет вид:

где $v$$v$ – некоторая константа пропорциональности (excluded volume parameter). Подставляя явные выражения для потенциала и для линейной плотности полимеров, приходим к соотношению:

где $\theta (h-x)$$\theta(h-x)$ в правой части учитывает, что выражение ($\text{25}$$\ref{eq:density}$) имеет смысл только при $x<h$$x<h$.

Упражнение 4. Закончите построение теории среднего поля и найдите $H$$H$ и $\psi (h)$$\psi(h)$.

Таким образом, высота щетки растет линейно с длиной $N$$N$ полимерных цепей. Полученные результаты находятся в прекрасном соответствии с результатами численного моделирования. Подробности можно найти в работе Milner-Witten-Cates, EPL 1988.