$$$\def \bm#1{\boldsymbol#1}$

Радиус гирации гауссовой цепи

Идеальная цепь

Полимерами называются длинные молекулы (макромолекулы), построенные из повторяющихся строительных блоков – мономеров, связанных химическими связями в единую цепочку. Хорошо известные примеры – ДНК и полиэтилен. Длина человеческого генома составляет порядка 2 метров. Как он размещается в клеточном ядре размером порядка 5 микрон – отдельная задача. Полиэтилен – цепочка из молекул $-C{H}_2-C{H}_2-$$-CH_2-CH_2-$.

Простейшая модель полимера – свободно-сочлененная цепь, которая представляет из себя последовательность из $N$$N$ шарнирно соединенных жестких сегментов длины $b$$b$ каждый. Будем считать цепь идеальной, то есть пренебрежем взаимодействиями не связанных друг с другом сегментов.

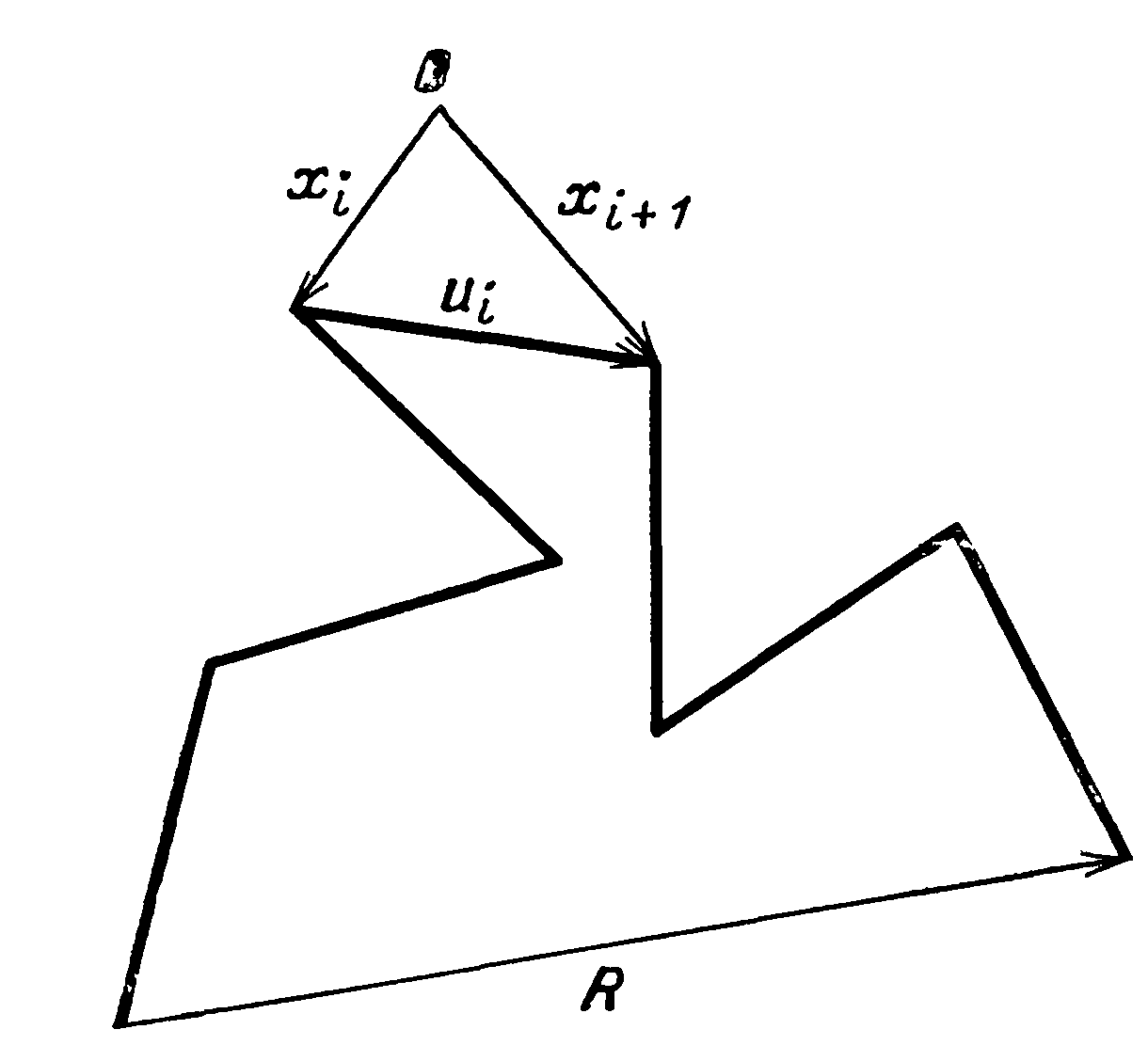
Пусть ${\mathbf{x}}_{\mathbf{i}}$$\bf x_i$ – радиус-вектор начала $i$$i$-го сегмента, также введем вектора связей ${\mathbf{u}}_{\mathbf{i}}\mathbf{=}{\mathbf{x}}_{\mathbf{i}\mathbf{+}\mathbf{1}}\mathbf{-}{\mathbf{x}}_{\mathbf{i}}$$\bf u_i = x_{i+1}-x_i$. Тогда

Чтобы охарактеризовать конформацию цепи введем в рассмотрение вектор, который соединяет ее начало и конец $\mathbf{R}=\sum _{i=1}^N{\mathbf{u}}_{\mathbf{i}}$${\bf R} = \sum_{i=1}^N {\bf u_i}$. Тогда легко показать, что

Более того, в силу центральной предельной теоремы при $N\gg 1$$N \gg 1$ для функции распределения $P_N(\mathbf{R})$$P_N({\bf R})$ получается распределение Гаусса:

Понятно, что по Гауссу будет распределено не только расстояние между концами цепи, но также и расстояние между любыми двумя не слишком близкими точками.

Конформационные свойства длинных цепей мало зависят от деталей их устройства на микро масштабах. Например, если в нашей исходной модели длины сегментов не постоянны, а выбираются из какого-то распределения с дисперсией $b^2$$b^2$, то окончательный ответ не изменится. Если между соседними сегментами цепи в модели заложена корреляция в пространстве, то она спадает с увеличением расстояния. Можно ввести понятие персистентной длины, на которой корреляциями можно пренебречь. Тогда всю цепь можно представить как совокупность некоррелированных участков, и мы возвращаемся к исходной задаче.

Гауссова цепь и случайные блуждания

Гауссовой цепью называют модель, в которой расстояние между любыми звеньями распределено по Гауссу. Кроме того, вместо дискретной версии полезно перейти к континуальному пределу. Запишем распределение Гаусса для расстояний между соседними звеньями

тогда вероятность конформации цепи равна

В этом случае становится очевидной аналогия с броуновским движением, только вместо времени выступает контурная длина вдоль полимерной цепи. Мы получаем, что каждая конформация цепи характеризуется вероятностью

где координата $0\le \tau \le N$$0 \leq \tau \leq N$ обозначает безразмерную контурную длину. Теперь мы можем анализировать конформации полимерной цепи с помощью формализма интеграла по траекториям.

Отметим, что наша модель полимера не очень хорошо соответствует действительности, поскольку в конформациях реального полимера отсутствуют самопересечения, в отличие от броуновской траектории. Язык функционального интеграла позволяет довольно легко модифицировать модель так, чтобы эффекты стерического взаимодействия можно было анализировать (self-avoiding random walk). Эта задача оказывается намного более сложной, и мы будем обсуждать ее дальше в нашем курсе.

Радиус гирации

Расстояние между концами полимера дает правильные представления о его размерах, но экспериментальными методами обычно измеряются другие характеристики. Например, упругое рассеяние света от разбавленного полимерного раствора позволяет измерять средний квадрат радиуса гирации

Упражнение 1. Покажите, что оба определения радиуса гирации тождественны друг другу.

Упражнение 2. Вычислите средний квадрат радиуса гирации для гауссовой цепи.

Решение. В континуальном пределе сумму следует заменить на интеграл

$$\begin{array}{}\text{(8)}& ⟨R_g^2⟩={\displaystyle \frac{1}{2N^2}}{\int }_0^{N}d{\tau }_1{\int }_0^{N}d{\tau }_2⟨(\mathbf{r}({\tau }_1)-\mathbf{r}({\tau }_2){)}^2⟩.\end{array}$$

Теперь воспользуемся тем, что расстояние между звеньями цепи ${\tau }_1$$\tau_1$ и ${\tau }_2$$\tau_2$ распределены по Гауссу, поэтому находим $⟨(\mathbf{r}({\tau }_1)-\mathbf{r}({\tau }_2){)}^2⟩=b^2|{\tau }_1-{\tau }_2|$$\left\langle ({\bf r}(\tau_1) - {\bf r}(\tau_2))^2 \right\rangle = b^2 |\tau_1-\tau_2|$. В итоге получаем

$$\begin{array}{}\text{(9)}& ⟨R_g^2⟩={\displaystyle \frac{b^2}{N^2}}{\int }_0^{N}d{\tau }_1{\int }_0^{{\tau }_1}d{\tau }_2({\tau }_1-{\tau }_2)={\displaystyle \frac{N{b}^2}{6}}.\end{array}$$

Интеграл по конформациям

Функция распределения для квадрата радиуса гирации на языке функционального интеграла может быть записана в виде

Для удобства перейдем к переменной $s=\tau /N$$s=\tau/N$, которая изменяется в пределах $0\le s\le 1$$0 \leq s \leq 1$:

Дельта функцию перепишем с помощью соотношения

и тогда получаем

где

имеет смысл характеристической функции. Ее разложение в ряд Тейлора определяет моменты случайной величины $R_g^2$$R_g^2$, а разложение в аналогичный ряд Тейлора функции $\ln K(\xi )$$\ln K(\xi)$ – кумулянты.

Характеристическая функция

Преобразуем выражение для характеристической функции к виду

где ${\omega }^2(\xi )=2N{b}^{2}i\xi /3$$\omega^2 (\xi) = 2Nb^2 i \xi/3$. Последнее слагаемое преобразуем с помощью формулы

что приводит нас к выражению

Теперь функциональный интеграл имеет Гауссов вид и может быть вычислен точно.

При вычислении функционального интеграла мы считаем, что $\mathbf{r}(0)=0$${\bf r}(0)=0$ и $\mathbf{r}(1)=\mathbf{R}$${\bf r}(1)={\bf R}$, кроме того по положению конца полимера $\mathbf{R}$$\bf R$ также подразумевается интегрирование. Мы будем производить вычисления с точностью до нормировочной константы, которая определится из условия $K(0)=1$$K(0)=1$. В итоге нам надо вычислить:

где

Вычисление производим стандартным образом. Вектор $\mathbf{r}(s)$${\bf r}(s)$ представляем в виде суммы "классической" или седловой траектории ${\mathbf{v}}_{SP}(s)$${\bf v}_{SP}(s)$ и флуктуаций $\rho (s)$${\bf \rho}(s)$ относительно этого главного пути, $\mathbf{r}(s)={\mathbf{v}}_{SP}(s)+\rho (s)$${\bf r}(s) = {\bf v}_{SP}(s)+{\bf \rho}(s)$. Граничные условия на вектор $\rho$${\bf \rho}$ нулевые. В итоге ответ принимает вид:

Флуктуационный фактор

Вычисление флуктуационного фактора сводится к взятию интеграла

которое может быть выполнено, например, методом Фурье (см. семинар №3). С точностью до константы ответ равен

Степень 3/2 вместо стандартной 1/2 учитывает то обстоятельство, что вектор $\rho$$\rho$ трехмерный.

Седловая точка

Седловая траектория определяется из уравнений Эйлера-Лагранжа

откуда получаем, что

Теперь вычисляем соответствующий вклад в действие:

Финальное вычисление

Нам осталось вычислить интеграл:

Сперва вычисляем интеграл по $\mathbf{R}$${\bf R}$, а затем по $\mathbf{x}$${\bf x}$

Теперь вспоминаем, что ${\omega }^2(\xi )=2N{b}^{2}i\xi /3$$\omega^2 (\xi) = 2Nb^2 i \xi/3$ и восстанавливаем константу из условия $K(\xi =0)=1$$K(\xi=0)=1$. Окончательно получаем:

Теперь можно найти моменты квадрата радиуса гирации, воспользовавшись разложением

В нашем случае:

и таким образом

Упражнение 3. Рассмотрите Гауссову цепь, у которой начало и конец сведены в одну точку (броуновский мост). Вычислите $K(\xi )$$K(\xi)$ для такой петли и определите $⟨R_g^2⟩$$\langle R_g^2 \rangle$.

Ответ. $K(\xi )={\left({\displaystyle \frac{\omega }{2\sin (\omega /2)}}\right)}^3$$K(\xi) = \left( \dfrac{\omega}{2 \sin (\omega/2)} \right)^3$, $⟨R_g^2⟩=N{b}^2/12$$\langle R_g^2 \rangle = Nb^2/12$.

Функция распределения

Теперь вернемся к выражению ($\text{13}$$\ref{eq:1}$) и вычислим $P(R_g^2)$$P(R_g^2)$. Используя найденный ответ для характерисической функции, получаем:

Здесь мы ввели обозначение ${\alpha }^2=R_g^2/⟨R_g^2⟩$$\alpha^2 = R_g^2/\langle R_g^2 \rangle$.

Упражнение 4. Интеграл можно вычислить методом перевала в пределах ${\alpha }^2\gg 1$$\alpha^2 \gg 1$ и ${\alpha }^2\ll 1$$\alpha^2 \ll 1$. Покажите, что для функции распределения получаются асимптотические выражения:

$$\begin{array}{}\text{(33)}& P(R_g^2)\simeq {\displaystyle \frac{e^{3/2}{\pi }^{5/2}}{N{b}^2}}\alpha \exp [-{\displaystyle \frac{{\pi }^2{\alpha }^2}{4}}],\alpha \gg 1,\end{array}$$

$$\begin{array}{}\text{(34)}& P(R_g^2)\simeq 54\sqrt{{\displaystyle \frac{6}{\pi }}}{\displaystyle \frac{{\alpha }^{-6}}{N{b}^2}}\exp [-{\displaystyle \frac{9}{4{\alpha }^2}}],\alpha \ll 1.\end{array}$$

Указание: M. Fixman, "Radius of Gyration of Polymer Chains", J. Chem. Phys. 36, 306 (1962);