Эффект Ааронова-Бома
Список литературы:
- R. Rattazzi, "The Path Integral approach to Quantum Mechanics", глава 5.3.
- A. Wipf, "Path Integrals", глава 5.
Эффект Ааронова-БомаЭлектромагнитный потенциалПропагатор частицы в магнитном полеДискретизация функционального интегралаЭффект Ааронова-Бома
Электромагнитный потенциал
Заряженная частица реагирует на присутствие электрического и магнитного полей – она ускоряется и/или ее траектория изгибается. В пустоте электрическое и магнитное поле удовлетворяют уравнениям Максвелла
и в курсе теории поля было показано, что поля можно выразить через компоненты 4-потенциала:
При этом у студентов обычно складывается впечатление, что векторный потенциал
Однако, это утверждение (как мы сегодня убедимся) является неверным. Рассмотрим бесконечно длинную цилиндрическую оболочку, такую что частицы не могут проникать внутрь ее. Тогда пропагатор частиц описывается уравнением Шредингера с граничным условием
Предположим теперь, что мы создали внутри цилиндра магнитное поле. Интуитивно кажется, что пропагатор частиц за пределами оболочки не изменится, поскольку магнитное поле
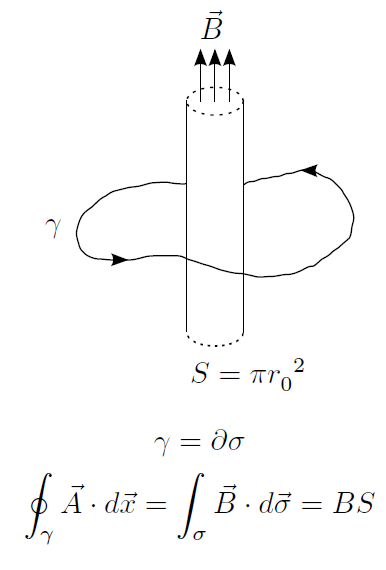
Отличие этих двух ситуаций заключается в том, что в случае с магнитным полем векторный потенциал
где
Пропагатор частицы в магнитном поле
Гамильтониан заряженной частицы в магнитном поле
поэтому для Лагранжиана мы можем записать
Интегрирование по импульсам выполняется тривиально и мы приходим к выражению для пропагатора
Дискретизация функционального интеграла
На примере этого действия полезно обсудить в какой точке пространства следует брать значение вектор-потенциала
где параметр
Переходим к новой переменной интегрирования
Из-за первого экспоненциального множителя интеграл набирается при малых
Теперь интегралы можно вычислить в явном виде
и мы получаем:
что при переходе к пределу
Правая часть должна совпадать с гамильтонианом
откуда мы немедленно получаем
Упражнение 1. Покажите, что внешнее усреднение
тоже приводит к правильному уравнению Шредингера.
Эффект Ааронова-Бома
Теперь достаточно просто увидеть, что
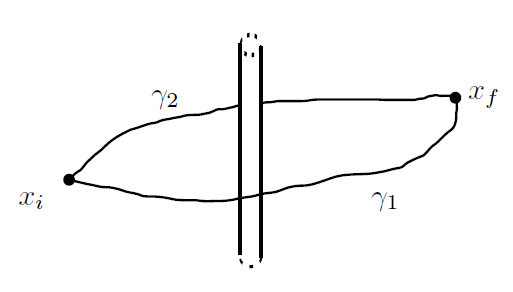
Эти пути дают следующие вклады в пропагатор
где
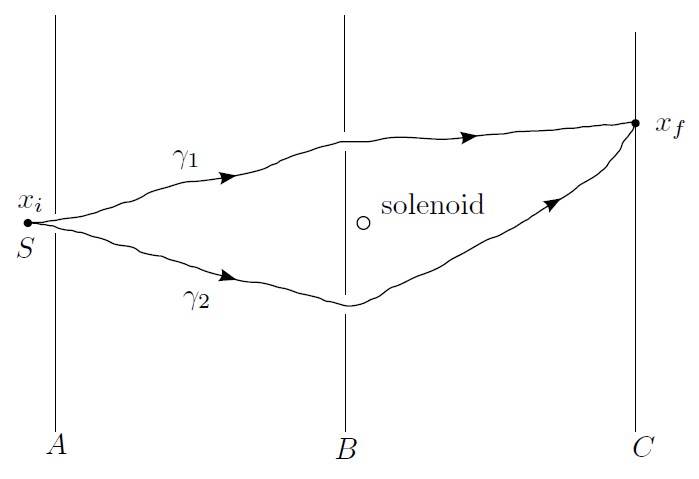
Эту разность фаз можно наблюдать экспериментально. Рассмотрим эксперимент с двумя щелями в присутствии соленоида. Магнитный поток создает дополнительную разность фаз, что приводит к сдвигу полос интерференционной картины.